Search Algorithm Demo: Overview

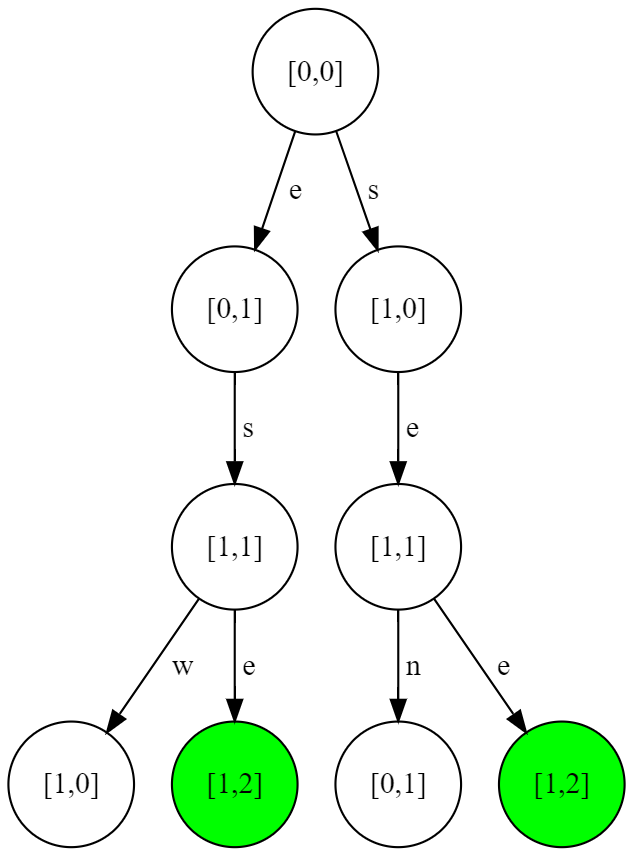
If cycles are permitted (that is, we don't care whether we return to a previously visited cell), then the associated search tree will be infinite in depth. E.g., repeating the actions e(ast), w(est) will generate one infinite branch of the tree.

Search Procedures

All of the search procedures proceed by constructing a search tree at runtime. The trees are made up of nodes with the following properties (as needed, other properties might be present e.g., node.DEPTH, node.HEURISTIC).

• node.STATE: The problem state associated with the node;
• node.PARENT: A reference to this node's parent node in the search tree;
• node.ACTION: The action applied to the state associated with node.PARENT to yield this node;
• node.PATH-COST: The total cost of the sequence of actions leading from the initial state to node.STATE.

The procedures also make use of a problem data structure which encodes the initial state of the problem (problem.INITIAL), provides a goal test function (problem.IS-GOAL), and encodes a transition function mapping states and actions to other states. An EXPAND function takes the problem and a search tree node as input and returns a set of children nodes representing the states immediately reachable from the parent node's state.

The Frontier and Reached States

The procedures incrementally construct the search tree, starting with a single root and examining each node to determine whether it represents a goal state. Nodes to be examined are stored in a collection called the frontier and removed (popped) one by one. If the current node removed corresponds to a goal state, it is returned by the procedure (the solution path can be reconstructed by following the node.PARENT references to the root of the tree). If it is not a goal state, the node is expanded and its children added to the frontier.

The different search procedures use different data structures to encode the frontier, and this largely controls the execution of the search.

A separate lookup table keeps track of which states have been reached during the search. As nodes are generated by the search, an entry for the corresponding state is added to the table. Only a single entry for each state will be stored at any given time, and it holds a reference to the node of the search tree having the lowest path-cost to that state.

Note: It is important to call attention to when states are marked as reached. As described here and in AIMA 4E, a node is marked reached at the time it is generated rather than when it is removed from the frontier and expanded. The earlier edition (AIMA 3E) instead used the term explored set (also closed list) to refer to states with nodes which have been expanded. As is clear from their definitions, the reached set and the explored set do not necessarily identify the same set.

A summary of the different search procedures is given below.

Breadth First Search (BFS)

For Breadth First Search (BFS), a first-in-first-out (FIFO) queue is used to store the frontier, and this naturally leads to all nodes at depth i being removed from the frontier before any of depth i+1.

Breadth First Search

      function BREADTH-FIRST-SEARCH(problem)
          node ← NODE(problem.INITIAL)
          if problem.IS-GOAL(node.STATE) then return node
          frontier ← a FIFO queue, with node as an element
          reached ← {problem.INITIAL}
          while not IS-EMPTY(frontier) do
              node ← POP(frontier)
              for each child in EXPAND(problem, node) do
                  s ← child.STATE
                  if s is not in reached then
                      if problem.IS-GOAL(s) then return child
                      add s to reached
                      add child to frontier
          return failure
      

Unlike the other search procedures discussed here, Breadth First Search performs a goal test on a node before it is added to the frontier. All of the other algorithms peform the goal test after the node is removed from the frontier. The first goal node generated by BFS will be the shallowest, and since there is no other property used by BFS to distinguish goal states, there is no need to generate any more nodes. In fact, continuing to generate nodes and add them to the frontier would add to the running time and memory used by the agorithm. For the algorithms attempting to find the lowest-cost goal state, it makes sense to perform the goal test after the nodes are removed from the frontier (Why? Because the first goal generated is not necessarily the lowest-cost one).

The version of Breadth First Search presented above differs from AIMA 4E in that the goal test on a child is performed only if the child's associated state has not already been reached. This is the way it is done in AIMA 3E as well. In AIMA 4E, the goal test is performed before checking to see whether the associated state has been reached. Arguably, it is better to to test to see if a state has been reached before performing a goal-test on it. This is because all but the last goal test will fail. By performing the test only after the reached test has been performed, some unnecessary work will have been avoided.

Best First Search and Uniform Cost Search (UCS)

Best First Search procedures use a priority queue sorted using some node property (path-cost, heuristic value, depth, etc.). Nodes with lower values are removed before those with higher values. For UCS, the queue is sorted according to the path-cost g(n) of each node n. Also, for Best First Search, the goal-test is performed on a node after it has been removed from the frontier.

Best First Search and Uniform Cost Search (UCS)

 
      function BEST-FIRST-SEARCH(problem, f)      
          node ← NODE(STATE=problem.INITIAL)
          frontier ← a priority queue ordered by f, with node as an element
          reached ← a lookup table, with one entry with key problem.INITIAL and value node
          while not IS-EMPTY(frontier) do
              node ← POP(frontier)
              if problem.IS-GOAL(node.STATE) then return node
              for each child in EXPAND(problem, node) do
                  s ← child.STATE
                  if s is not in reached or child.PATH-COST < reached[s].PATH-COST then
                      reached[s] ← child
                      add child to frontier
          return failure
          
      function UNIFORM-COST-SEARCH(problem)
          return BEST-FIRST-SEARCH(problem, PATH-COST)    
      

As shown, a node is added to the frontier only if its corresponding state has not been reached (that is, no other node for the same state was created earlier in the search) or if the path-cost for the node is lower than for any other node for the same state. The path-cost check is needed to ensure that the lowest cost solution is found (there is no guarantee that the first node generated for a state corresponds to the best path to the state).

Uniform Cost search is both complete and optimal (guaranteed to yield an optimal solution), provided the step costs between states are all above some positive lower bound (i.e., step costs cannot be arbitrarily small or negative) and the branching factor of nodes is finite.

Note that in the procedure as written, if a node with a better path-cost is found and added to the frontier, the inferior nodes remain in the frontier. As an alternative, the inferior nodes can be removed (the algorithm for UCS in AIMA 3E does this). This would potentially prevent repeatedly examining dead end paths through the same state.

Graph Search and Tree Search

If the test child.PATH-COST < reached[s].PATH-COST is removed from Best First Search, then the result is sometimes called a simple Graph Search. AIMA 4E does not present pseudocode for it (AIMA 3E does), but it might look as follows when using the same pseudocode notation.

Graph Search

 
      function GRAPH-SEARCH(problem, f)      
          node ← NODE(STATE=problem.INITIAL)
          frontier ← a priority queue ordered by f, with node as an element
          reached ← a lookup table, with one entry with key problem.INITIAL and value node
          while not IS-EMPTY(frontier) do
              node ← POP(frontier)
              if problem.IS-GOAL(node.STATE) then return node
              for each child in EXPAND(problem, node) do
                 s ← child.STATE
                 if s is not in reached then
                     reached[s] ← child
                     add child to frontier
          return failure
      

This simple graph search procedure cannot be used for UCS, since doing so would elminate the guarantee that the lowest cost solution is ultimately found.

If the reached test is removed as well, then the result is TREE-SEARCH. As noted earlier, without the reached test, it is possible for the search to cycle endlessly even if the underlying state space is finite.

Tree Search

 
      function TREE-SEARCH(problem, f)      
          node ← NODE(STATE=problem.INITIAL)
          frontier ← a priority queue ordered by f, with node as an element          
          while not IS-EMPTY(frontier) do
              node ← POP(frontier)
              if problem.IS-GOAL(node.STATE) then return node
              for each child in EXPAND(problem, node) do
                  add child to frontier
          return failure
      

Greedy Best First Search (GBF)

Greedy Best First Search is a best first search procedure in which the priority queue is sorted in increasing order of heuristic values h(n), where h(n) is an estimate of the least cost to get from node n's state to the closest goal state. In GBF, nodes with lower h values are selected and removed from the frontier before those with higher values.

Since the selection of nodes is not based on path-cost, it is arguable that using the simple GRAPH-SEARCH makes more sense for GBF than Best First Search. Indeed, If the path-cost check is used in conjunction with a bad heuristic, then GBF can revisit many more states than if the path-cost check was omitted. Even with a reasonable heuristic, the two variants will perform differently on some of the example problems included here (in some cases, the first variant does investigate many paths to the same state).

A* Search

A* is a Best First Search Algorithm using f(n) = g(n) + h(n) to sort the priority queue. Again, g(n) is the actual total cost of getting from the initial state to n, while the heuristic function h(n) yields the estimated cost of getting from n to the goal state closest to n. Under the same assumptions of UCS and also that the heuristic function used is admissible (does not overestimate the true cost to reach a goal state from n), A* is both complete and optimal.

Given h and g as described above, A* can be defined as follows.

A* Search

 
      function A-STAR-SEARCH(problem)
          f, the evaluation function f(n) = g(n) + h(n)
          return BEST-FIRST-SEARCH(problem, f)       
      

Depth First Search, Depth-Limited Search, and Iterative Deepening

Depth First Search (DFS) can be implemented as a Best First Search using -1*node.DEPTH as the sorting criterion for the priority queue (a deeper node will have a value closer to -∞ and so be less than a shallower node). However, it is more efficient to simply use a last-in-first-out (LIFO) stack, which will always have a node of greatest depth as its topmost element.

Also, since DFS is not guaranteed to be complete or optimal, there seems little reason to include the path-cost check. A variation of graph search where this is the case is shown below. It is not presented in AIMA 4E.

Depth First Search (DFS)

      function DEPTH-FIRST-SEARCH(problem)
          node ← NODE(STATE=problem.INITIAL)
          frontier ← a LIFO stack, with node as an element
          reached ← a lookup table, with one entry with key problem.INITIAL and value node
          while not IS-EMPTY(frontier) do
              node ← POP(frontier)
              if problem.IS-GOAL(node.STATE) then return node
              for each child in EXPAND(problem, node) do
                 s ← child.STATE
                 if s is not in reached then
                     reached[s] ← child
                     add child to frontier
          return failure
      

AIMA 4E does not present any version of DFS explicitly. However, it does present both depth-limited search and iterative deepening. These are shown below.

Depth-Limited and Iterative Deepening Search

      function ITERATIVE-DEEPENING-SEARCH(problem)
          for depth = 0 to ∞ do
              result ← DEPTH-LIMITED-SEARCH(problem, depth)
              if result != cutoff then return result

            function DEPTH-LIMITED-SEARCH(problem, maxdepth) 
                frontier ← a LIFO queue (stack) with NODE(problem.INITIAL) as an element
                result ← failure
                while not IS-EMPTY(frontier) do
                    node ← POP(frontier)
                    if problem.IS-GOAL(node.STATE) then return node
                    if DEPTH(node) > maxdepth then
                        result ← cutoff
                    else if not IS-CYCLE(node) do
                        for each child in EXPAND(problem, node) do                           
                            add child to frontier
                return result
      

Here, rather than using a lookup table to store reached states, an on-path IS-CYCLE test is performed. While such a cycle check is often paired with DFS rather than keeping a reached lookup table, it results in combinatorial explosion in simple grid environments such as those in the demo (because of the many unique a cycle-free paths between two points in a grid). In such environments, it is better to use the lookup table to keep track of visited states. The on-path cycle check is much more memory efficient than storing the full reached set, however; apart from the frontier, only the current path needs to be kept in memory.

Note that as presented above, the cycle test is performed after a node is popped from the frontier and after it is goal-tested. What this means is that nodes for known non-goal states can be placed onto the frontier. As an alternative, the goal-test could be done early, before nodes are ever placed on the frontier. In both cases, a node identifying a cycle is never expanded. The two versions are nevertheless not equivalent, can produce different paths, and can have significantly different running times.

Implementations

The following search procedure variants are included in this demo.

• Depth First Search (DFS): A simple graph search; nodes are added to the frontier only if their states have not already been reached. Deeper nodes in the search tree are selected for expansion before shallower nodes.
• Depth First Search (On-path cycle check): A version of DFS using an on-path cycle check rather than a lookup table of reached states. A version performing the cycle test after removing a node from the frontier if presented, as is one which performs the test before a node is added to the frontier.
• Breadth First Search (BFS): A graph search using an early goal test. Shallower nodes in the search tree are selected for expansion before deeper nodes. A version performing a late goal test (after removal from the frontier) is also provided.
• Breadth First Search (late goal test): A variant of BFS performing a goal test only after nodes are removed from the frontier rather than before. This variant of BFS is generally worse than the variant performing an early goal test, in the sense that it may needlessly generate an additional layer of nodes in the search tree.
• Iterative Deepening: A graph search version of iterative deepening using a reached lookup table. This is like DFS but with an incrementally increasing maximum depth limit for the search.
• Uniform Cost Search (UCS): A best first search using path-cost g(n) to select nodes. A reached state lookup table is kept, and a node for an already reached state can be added to the frontier provided it has a lower path cost.
• Uniform Cost Search (remove redundant paths): A variant of UCS in which higher path-cost nodes for a state are removed from the frontier as lower-cost ones are added.
• Greedy Best First Search (GBF): A best first graph search using a heuristic function h(n) to select nodes from the frontier.
• A*: A best first graph search using the sum of the path-cost and heuristic value to select nodes (i.e., f(n) = g(n) + h(n)).
• Depth First Search (Tree): A tree search version of DFS. No reached table is kept.
• Breadth First Search (Tree): A tree search version of DFS. No reached table is kept.
• Uniform Cost Search (Tree): A tree search version of UCS. No reached table is kept.
• Greedy Search (Tree): A tree search version of GBF. No reached table is kept.
• Iterative Deepening (On-path cycle check): A version of iterative deepening using an on-path cycle check instead of a reached lookup table. On the 2D grid problems of the demo, this will generally require significantly more steps than the variant using a reched set.

The different variations can perform quite differently in different settings. Users of the demo are encouraged to investigate the performance of each procedure on the sample problems, paying attention to the number of steps required to discover a solution, the path-cost of the solution found, the size of the frontier and visited state sets, etc.

Images

The agent icon is from the 1984 game Dragonfire for the TRS-80 Color Computer (CoCo).